While defining a matrix we must define their order. e.g. 3 by 2 matrix i.e. rectangular array of 3 rows and 2 columns. Represented as ![]() OR
OR ![]()
Element of matrix A: ![]()
Type of Matrices
Row Matrix or Row Vector: Matrix having only one row. e.g row matrix of order 1×4
A = [ 1 2 -1 -2]
Column Matrix or Column Vector: Matrix having only one column e.g column matrix of order 3×1
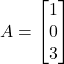
Square Matrix: The number of rows is equal to the number of columns. The square matrix of order n is also called the n-rowed square matrix.
Diagonal Element: Only a square matrix has the diagonal element i.e ![]() where i=j e.g
where i=j e.g ![]()
Principal Diagonal or Leading Diagonal of the Matrix: The line along which diagonal elements lie.
Diagonal Matrix: A square matrix where all elements are zero except those in the leading diagonal i.e ![]() where
where ![]()
Denoted by A = diag[1,5,11]

Scalar Matrix: A square matrix where all diagonal elements are the same but not 0.
Identity or Unit Matrix: A square matrix where all diagonal elements are 1 and other elements are 0. The Identity matrix of order n is denoted by ![]() . Following is the Identity matrix of order 3
. Following is the Identity matrix of order 3
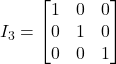
Null Matrix: The matrix whose all elements are 0. Represented as 0
Upper Triangular Matrix: All elements are below the main diagonal is 0. i.e. ![]() where i>j
where i>j

Lower Triangular Matrix: All elements are above the main diagonal is 0. i.e. ![]() where j>i
where j>i
Strict Triangular Matrix: In the Upper and Lower triangular matrix even the element in the leading diagonal is also 0

Equality of Matrices
A=[![]() ]
]![]()
B=[![]() ]
]![]()
If A = B then m=r and n=s i.e. their order has to be the same. And the corresponding elements are equal.
Addition of Matrices
- Sum of two matrices is possible when both are of the same order
- The resulting matrix also will be of the same order
Property of Matrix Addition
Theorem-1: Commutative
A+B = B+A, A& B are of the same order
Theorem-2: Associative
A, B & C are of the same order
(A+B)+C = A+(B+C)
Theorem-3: Existence of Identity
NULL matrix is the identity element for matrix addition.
A+O = A = O+A
Theorem-4: Existence of Inverse
For every matrix, there exists a matrix -A, such that
A + (-A) = O = (-A) + A
-A is called the Additive Inverse of A
Theorem-5: Cancellation Laws
A, B & C are of the same order
A+B = A+C then, B= C Left Cancellation
B+A=C+A then B=C Right Cancellation
Scalar Multiplication
Let k be any number, called Scalar. The matrix obtained by multiplying every element of A by k is called the Scalar multiple of A by k. It is denoted by kA.
kA = [k![]() ]
]![]()
Properties of Scalar Multiplication
A=[![]() ]
]![]()
B=[![]() ]
]![]()
Matrices are of the same order. k & l are the scalar.
- k(A+B) = kA + kB
- (k+l) A = kA + lA
- (kl)A = l(kA) = k(lA)
- (-k)A=-(kA) = k(-A)
- IA = A
- (-1)A = -A
Subtraction of Matrices
A – B = A + (-B)
A & B are of the same order
Multiplication of Matrices
A & B can be multiplied if the number of columns of A is equal to the number of the rows in B. i.e
The order of A is m x n
The order of B is n x p
The order of the product is m x p
![]() = (i-th row A) (j-th column of B)
= (i-th row A) (j-th column of B)
i = 1,2,…,m j = 1,2,…,p
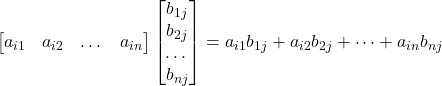
(1) ![]()
Properties of Matrix Multiplication
Theorem-1: Not Commutative
A = 3 x 2 B = 2 x 5
AB is possible but BA is not possible.
Theorem-2: Associative
(AB)C = A(BC)
Theorem-3: Distributive over matrix addition
A(B+C) =AB + AC
Theorem-4: If A = m x n order.![]() is the unit matrix of the column m
is the unit matrix of the column m![]() is the unit matrix of the row n
is the unit matrix of the row n![]() A=A=A
A=A=A![]()
Theorem-5: The product of a matrix with the NULL matrix is always a NULL matrix.
Note: The product of two matrices can be a NULL matrix when neither of them is a NULL matrix.
![]()
if AB is a NULL matrix then it is not necessary BA is also a NULL matrix.
Positive Integral Power of Square Matrix
 = A
= A


Note: Applicable only for square matrix
Matrix Polynomial
![]()
A is a square matrix
![]()
TBD

1st Matrix: 3Row1 +2Row2 = Row3 i.e 3rd matrix dependent on first two matrices. Therefore, Singular
2nd Matrix: Row1 – Row2 = Row3 i.e 3rd matrix dependent on first two matrices. Therefore, Singular
3rd Matrix: No relation i.e 3rd matrix not dependent on first two matrices. Therefore, Non-Singular
4th Matrix: 2Row1 = Row3 i.e 3rd matrix dependent on first matrix. Therefore, Singular
The Determinant (|A|)
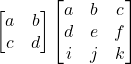
- Singular Matrices – If the determinant is 0 then matrices are Singular
- Non Singular Matrices – If the determinant is not 0 then matrices are Non Singular
For 2×2 matrix
|A| = a*d – b*c == 0 Singular
|A| = a*d – b*c != 0 Non Singular
For 3×3 matrix
|A| = a*(e*k – j* f) – b*(d*k – f*i) + c*(d*j – e* i) == 0 Singular
|A| = a*(e*k – j* f) – b*(d*k – f*i) + c*(d*j – e* i) != 0 Non Singular
Note: Shortcut to find determinant if all data below the diagonal elements are 0.
In this case determinant is the product of all diagonal element. e.g
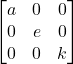
|A| = a*e*k



