Algebra

Linear Regression

Supervised Machine Learning

Linear Equations

(1) $\begin{equation*} w_1x_1^{(1)}+w_2x_2^{(1)}+\dots+{w_n}x_n^{(1)}+b=y^{(1)}\end{equation*}$

(2) $\begin{equation*} w_1x_1^{(2)}+w_2x_2^{(2)}+\dots+{w_n}x_n^{(2)}+b=y^{(2)}\end{equation*}$

$\dots$

(3) $\begin{equation*} w_1x_1^{(m)}+w_2x_2^{(m)}+\dots+{w_n}x_n^{(m)}+b=y^{(m)}\end{equation*}$

$w_1,w_2,\dots,w_n$ are weights

$x_1^{(1)},x_1^{(2)},x_1^{(m)}\dots$ are datasets

So in linear equation weight remain same but dataset varies.

System of Sentences

Non Singular System

Such system comprises of non contradictory statements. Which results in more info for analysis. e.g.

System-1

The dog is black.
The cat is yellow.

Both statements are providing unique information. In this system we can deduce some information which is not provided directly. e.g

Between the dog, the cat and the bird, one of them is red
What colour is the bird? [ This information is not there]

Singular System

This system have contradictory or redundant statements.

System-2

The dog is black.
The dog is black.

Redundancy information. Rank is the measure use to know how redundant the system is.

System-3

The dog is black.
The dog is white.

Contradictory information.

System of Equations

Non Singular System

a=apple
b=banana
numbers are price in rupee
a+b= 10
a+2b=12
we can deduce the price of a and b
If we draw line in cartesian plane the above two lines will intersect each other at one point. That will be the solution

Singular System

a+b=10
2a+2b=20
Redundant equations. There can be infinitely many solution e.g (3,7), (2,8), (2.1, 7.9)..
If we draw line in cartesian plane the above two lines will coincide with each.Therefore all points on those lines are solution.
a+b=20
2a+2b=24
Contradictory equations. No solution possible
If we draw line in cartesian plane the above two lines will be parallel to each other. That will be no solution.

Note: Constant in linear equation not important to determine if the equation is singular or non-singular.

Matrix

$\begin{bmatrix}1 & 0 & 1\\0 & 1 & 0\\3&2&3\end{bmatrix}\begin{bmatrix} 1 & 1 & 1\\1 & 1 & 2\\0&0&-1\end{bmatrix}\begin{bmatrix} 1 & 1 & 1\\0 & 2 & 2\\0&0&3\end{bmatrix}\begin{bmatrix} 1 & 2 & 5\\1 & 3 & -2\\2&4&10\end{bmatrix}$

1st Matrix: 3Row1 +2Row2 = Row3 i.e 3rd matrix dependent on first two matrices. Therefore, Singular

2nd Matrix: Row1 – Row2 = Row3 i.e 3rd matrix dependent on first two matrices. Therefore, Singular

3rd Matrix: No relation i.e 3rd matrix not dependent on first two matrices. Therefore, Non-Singular

4th Matrix: 2Row1 = Row3 i.e 3rd matrix dependent on first matrix. Therefore, Singular

The Determinant (|A|)

$\begin{bmatrix}a & b \\c & d\end{bmatrix}\begin{bmatrix}a & b & c\\d & e & f\\i & j & k\end{bmatrix}$

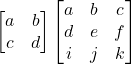
Singular Matrices – If the determinant is 0 then matrices are Singular
Non Singular Matrices – If the determinant is not 0 then matrices are Non Singular

For 2×2 matrix

|A| = a*d – b*c == 0 Singular

|A| = a*d – b*c != 0 Non Singular

For 3×3 matrix

|A| = a*(e*k – j* f) – b*(d*k – f*i) + c*(d*j – e* i) == 0 Singular

|A| = a*(e*k – j* f) – b*(d*k – f*i) + c*(d*j – e* i) != 0 Non Singular

Note: Shortcut to find determinant if all data below the diagonal elements are 0.

In this case determinant is the product of all diagonal element. e.g

$\begin{bmatrix}a & 0 & 0\\0 & e &0\\0 & 0 & k\end{bmatrix}$

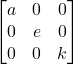
|A| = a*e*k

Linear Regression

Supervised Machine Learning

Linear Equations

System of Sentences

Non Singular System

Singular System

System of Equations

Non Singular System

Singular System

Matrix

The Determinant (|A|)

Table of Contents

You may also like to read

Matrices

Standard Identities

Popular content

contact us