At first, we sample ![]() in the
in the ![]() (
(![]() is odd) equidistant points around
is odd) equidistant points around ![]() :
:
![]()
where
Then we interpolate points
(1) 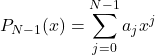
Its coefficients
(2) ![]()
Here are references to existing equations: (1), (6).
Here is reference to non-existing equation (??).
| City | Pin Code | State | Name | Surname |
|---|---|---|---|---|
| sds | sds | |||
| ds | s | |||
| ds | ssd | |||
| ds |
Matrix
[katex display=true]
\begin{bmatrix}
1 & 2 & 3\\
a & b & c
\end{bmatrix}
[/katex]
